Introduction
Matting refers to the process of extracting foreground object from an image. Matting tasks usually produces a "matte" that can be used to separate foreground from the background in a given image. Matte can also used to combine a given foreground on a different background to produce new plausible image. We've implement an image matting system with user-friendly interface. Two image mating algorithm including the close form solution method and the conjugate gradient method are adopted in our system.User interface
Close form solution algorithm requires only scribles from the users. We implement a user-friendly interfae for the users to add scribles onto the image. Users can also adjust the size of the brush to fastly select a wide range of area. The image below is how a user add scribbles to an image.
Close Form Solution
In Matting problem. An image is depicted as the combination of a foreground and background. Each pixels follow the matting equation:Ii = αi*Fi + (1-αi)*Bi,
where Ii, αi, Fi, Bi, respectively represents to the the composite value, the matte value, the foreground value, the back ground value of pixel i.All variable on the right of the matting equation are unknown. Hence the problem is under-constrained. So a rough segmentation of foreground and background is required to extract a good matte. This segmentation can be in form of trimap or scribbles. The close form solution is a scribble based matting algorithm. It makes two assumptions:(1) F and B are locally smooth over a small window. (2) Each of F and B is a linear mixture of two colors in a small window.
By assumption(1), we could rewrite the matting equation as:αi = a*Ii + b ∀i∈w, where w is a small window a = 1/F-B b = -B/F-B
Our goal is to find a set of parameters (α, a, b) that minimizes the cost function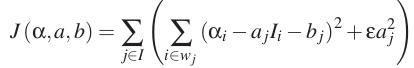
,where w is a small window.
A 3X3 window is adopted to enable propagation of the information between neighbouring pixels. The cost function is quadratic in α, a and b, with 3N unknowns for an image with N pixels. However, a and b may be eliminated , leaving us with a quadratic cost in only N unknown alpha values of the pixels:
J (α) = α’ L α, where a’ is the transpose of α
where L is an N × N matrix, whose (i, j)-th entry is:
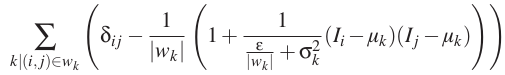For color images we replace the linear model with a 4D linear model assuming that for a small window each of F and B is a linear combination of two colors.
With 4D linear model the cost function is define as:
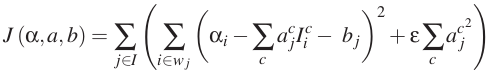The equation for Matting Laplacian in color line model becomes:
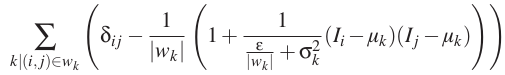The cost function can be optimized by solving a sparse linear system:
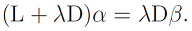
Conjugate gradient method
We already know the final step of close-form algorithm is to solve the sparse linear system. Conjugate gradient (CG) is another way to solve it. The conjugate gradient method is an iterative, so it can be applied to sparse systems that are too large to be handled by direct methods. (like mention above) The algorithm is detailed below for solving Ax = b where A is a real, symmetric, positive-definite matrix. The input vector x0 can be an approximate initial solution or 0. In our project, A=(L+lambda*D) and B = lambda*D*beta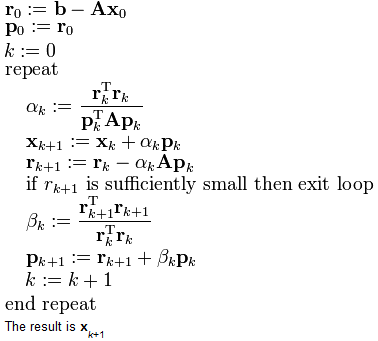
Experiment Result
First Result is a picture of a kid. The foreground and background has a relatively bigger contrast, such as the kid’s brown hair and her mothers green clothes. Therefore, we don’t need to draw a lot of scribbles to achieve our result.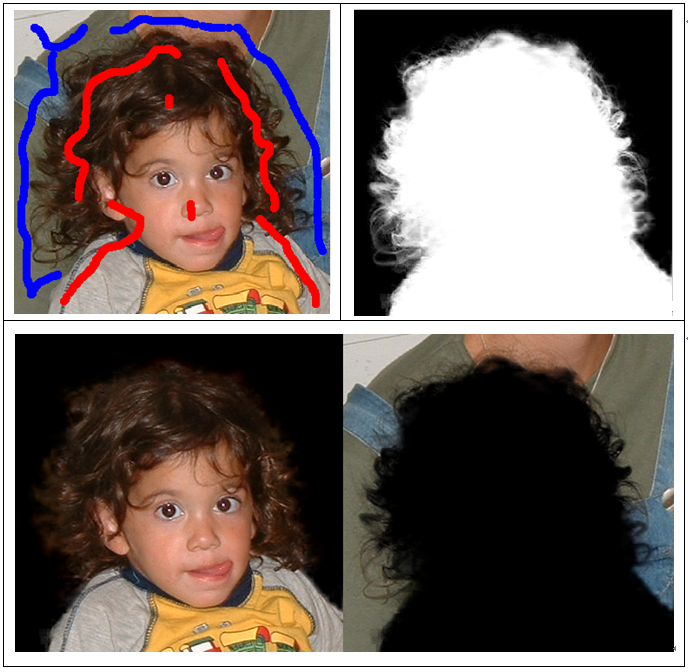
Second Result is a picture of a pineapple. Since it’s texture is similar to the back ground, we can find the scibbles in the first picture sets aren’t enough. The pixels in the upper left side cannot be distinguished properly. Then, we add some scibbles in the second picture sets to make the result better.
Third Result is a picture of a plant. The leaves of the plant have a lot of boundaries along with the background. Because that the color is so different between them, the result is still good.
